Step-by-step explanation:
The cross-sectional area of the specimen is calculated as follows.
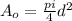
=
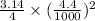
=
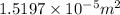
Equation of stress is as follows.
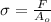
And, the equation of strain is as follows.
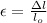
Hence, the Hook's law is as follows.
E =
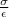
E =
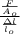
=

or,
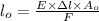
=
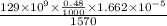
= 0.6554 m
or,
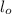 = 655.4 mm
= 655.4 mm
Thus, we can conclude that the maximum length of the specimen before deformation if the maximum allowable elongation is 0.48 mm is 655.4 mm.