Answer:
(a) 9.402 meters above the roof
(b) Velocity is 31.193 m/s just before hitting the ground
(c) Horizontal distance traveled is 104.2 meters
Step-by-step explanation:
Let's first find the horizontal and vertical velocity components of the rock when it is thrown. These are:
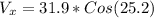
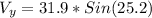
So we have,
Horizontal velocity = 28.864 m/s
Vertical velocity = 13.582 m/s
Now let's solve the three parts with this information:
(a) To find the maximum height, we need to use the fact that vertical velocity at this point will be zero, as the rock is just about to start falling downward. So we have:
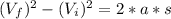
where
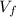 is the final velocity = 0 m/s
is the final velocity = 0 m/s
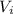 is the initial velocity = 13.582 m/s
is the initial velocity = 13.582 m/s
and a is the acceleration = -9.81 m/s^2
Solving, we get:
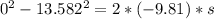
s = 9.402 m (distance above roof)
(b) Using the maximum height from (a), we can solve the following equation:
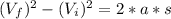
where
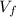 is the final velocity we need to find,
is the final velocity we need to find,
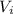 is the initial velocity = 0 m/s (from maximum height)
is the initial velocity = 0 m/s (from maximum height)
a is the acceleration = 9.81 m/s^2
and s = 14.9 + 9.402 = 24.302 m
Solving, we get:

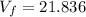 m/s
m/s
As this is just the vertical velocity, to find the total velocity we have:
V =
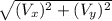
V =
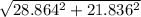
V = 36.193 m/s (Total velocity just before it hits the ground)
(c) To solve for this, we need to know the total time for this projectile motion, we can calculate this as follows:
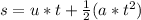
here, s = -14.9 m
u = 13.582 m/s (initial vertical velocity)
a = - 9.81 m/s^2 (acceleration due to gravity)
Solving, we get:
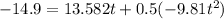
and get the answers:
t1 = 3.61 s
t2 = -0.84 s
Since t2 isn't possible, our total time is t1 = 3.61 seconds.
Using this and our horizontal velocity, we can find the total distance traveled:
Distance = 28.864 * 3.61
Distance = 104.2 m (horizontal)