Question

A man stands on the roof of a building of height 14.9 m and throws a rock with a velocity of magnitude 31.9 m/s at an angle of 25.2 ∘ above the horizontal. You can ignore air resistance.Assume that the rock is thrown from the level of the roof.

Calculate the maximum height above the roof reached by the rock.

Calculate the magnitude of the velocity of the rock just before it strikes the ground.

Calculate the horizontal distance from the base of the building to the point where the rock strikes the ground.

Answer 1

(a) 9.402 meters above the roof

(b) Velocity is 31.193 m/s just before hitting the ground

(c) Horizontal distance traveled is 104.2 meters

Step-by-step explanation:

Let's first find the horizontal and vertical velocity components of the rock when it is thrown. These are:

`V_x=31.9 * Cos(25.2)`

`V_y=31.9*Sin(25.2)`

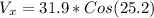
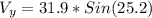
So we have,

Horizontal velocity = 28.864 m/s

Vertical velocity = 13.582 m/s

Now let's solve the three parts with this information:

(a) To find the maximum height, we need to use the fact that vertical velocity at this point will be zero, as the rock is just about to start falling downward. So we have:

`(V_f)^2 - (V_i)^2 = 2*a*s`

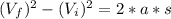
where
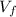`V_f` is the final velocity = 0 m/s

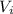`V_i` is the initial velocity = 13.582 m/s

and a is the acceleration = -9.81 m/s^2

Solving, we get:

`0^2-13.582^2=2*(-9.81)*s`

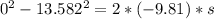
s = 9.402 m (distance above roof)

(b) Using the maximum height from (a), we can solve the following equation:

`(V_f)^2 - (V_i)^2 = 2*a*s`

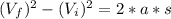
where
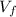`V_f` is the final velocity we need to find,

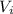`V_i` is the initial velocity = 0 m/s (from maximum height)

a is the acceleration = 9.81 m/s^2

and s = 14.9 + 9.402 = 24.302 m

Solving, we get:

`(V_f)^2 - (0)^2 = 2*(9.81)*(24.302)`

`V_f = 21.836` m/s

As this is just the vertical velocity, to find the total velocity we have:

V =
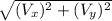
`√((V_x)^2+(V_y)^2)`

V =
`√(28.864^2 + 21.836^2)`

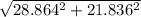
V = 36.193 m/s (Total velocity just before it hits the ground)

(c) To solve for this, we need to know the total time for this projectile motion, we can calculate this as follows:

`s=u*t+(1)/(2) (a*t^2)`

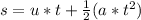
here, s = -14.9 m

u = 13.582 m/s (initial vertical velocity)

a = - 9.81 m/s^2 (acceleration due to gravity)

Solving, we get:

`-14.9 = 13.582t+0.5(-9.81t^2)`

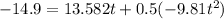
and get the answers:

t1 = 3.61 s

t2 = -0.84 s

Since t2 isn't possible, our total time is t1 = 3.61 seconds.

Using this and our horizontal velocity, we can find the total distance traveled:

Distance = 28.864 * 3.61

Distance = 104.2 m (horizontal)