Question

A circuit board manufacturer estimates the yearly demand to be 1,000,000. It costs $400 to set up the 3D printer for the circuit board, plus $10 for each one produced. If it costs the company $2 to store a circuit board for a year, how many should be produced at a time and how many production runs will be needed to minimize costs

Answer 1

The Question here is about Minimizing Inventory Costs. It is a topic treated under the Supply Chain Management. It is a concept very crucial to the work of Supply Chain Managers, Operations Managers as well as Accounting and Finance professionals who are tasked with minimizing cost whilst maximizing profit.

Inventory costs may be reduced by:

• Avoid Minimum Order Quantities

• Know Your Reorder Point.

• Organize Your Warehouse.

• Get Rid of Obsolete Stock.

• Implement a Just-in-Time Inventory System.

• Use Consignment Inventory.

• Reduce Your Lead Time.

• Monitor KPIs

The minimum inventory cost according to the factors given in the question above is:

See how we got there below:

Explanation:

Step 1

Number of Circuit Boards expected to be sold in a year = 1,000,000

Cost of each Circuit Board = $10

Cost of Setting up the 3D printer = $400

Cost of Storage for each Circuit board = $2

Step 2

Let

x = the number of circuit boards in each run

Storage Costs as in the question, an average of (
`(X)/(2)`) circuit boards are stored throughout the year, at a cost of $2 each, so annual storage costs are

Storage Costs =
`(X)/(2)`* 2 = x

Therefore Storage Costs = x

Production Costs The cost per run is given below:

Cost Per Run = (10x + 400) this is x Circuit Boards at $10 each, plus $400 set up costs

The 1,000,000 circuit boards at x circuit boards per run =
`(1,000,000)/(X)`

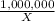
Therefore production costs are:

(Production Cost ) = (10x + 400) * (
`(1,000,000)/(X)`)

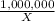The above expression is cost per run multiplied by number of runs

Total cost The total cost is storage cost plus production cost:

C(x) = x + (10x +400) (1,000,000/x)

Opening up the brackets we have

> C(x) = x + 10,000,000 + (40,000,000/x)

Step 3

For minimum cost the first derivative of the cost function will be equal to 0. Hence differentiating C(x) respect to x and equating to 0 gives:

C'(x) = x +
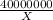`(40000000)/(X)` + 10,000,000 = 0

First Derivative =

1 - (40,000,000/
`X^(2)`) = 0

1 =
`X^(2)`/40,000,000

`X^(2)` = 40,000,000

X =
`√(40,000,000)`

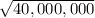
X = 6324.55532034

X is approximately equal to 6,325

So by the second derivative test,

C'' (X) =
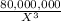`(80,000,000)/(X^(3) )` > 0

= 430.886938006 or approximately 431

Therefore

Now for the cost the total number of orders placed at a time will be

=
`(6,325)/(431)`

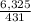
= 14.6751740139 or approximately 15

Step 4

Therefore for minimizing inventory cost, the order size should be 431 Circuit Boards per order, ordered 15 times in a year.

Cheers!

Answer 2

The manufacturer have to produce 20,000 circuit boards per run with 50 production runs

Step-by-step explanation:

Let x = number of circuit boards to be produced

An average of x/2 circuit boards are stored throughout the year at a cost of $2 each;

so annual storage cost = x/2*2 = x

Note: it costs $10 each to produce x circuit boards and $400 to set up

Therefore, The cost per run = 10x + 400

The 1,000,000 circuit boards at x circuit board per run would require 1000000/x runs.

Therefore, production costs = cost per run * production run

production costs = (10x + 400)*(1000000/x) = 10,000,000 + 400,000,000/x

Total cost C = storage cost + production cost

C = x + 10,000,000 + 400,000,000/x

Set c to zero and differentiate c with respect to x

0=1+0-400,000,000/x²

Therefore x = 20,000

Number of circuit boards that should be produced to minimize cost is 20,000

While the production runs needed = 1,000,000/x = 1,000,000/20,000= 50

The manufacturer have to produce 20,000 circuit boards per run with 50 production runs