Answer:
0.19mA
Step-by-step explanation:
Given;
Capacitor of capacitance = 4.07 μF
Resistor of resistance = 7.71 kΩ = 7.71 x 1000Ω = 7710Ω
Voltage = 1.50V
Since the capacitor is initially uncharged, it behaves like a short circuit. Therefore, the only element drawing current at that instant is the resistor. This means that the initial current in the circuit is the one due to (flowing through) the resistor.
And since there is negligible internal resistance, the emf of the battery is equal to the voltage supplied by the battery and is used to supply current to the resistor. Therefore, according to Ohm's law;
V = I x R ---------------(i)
Where;
V = voltage supplied or the emf
I = current through the resistor
R = resistance of the resistor
Substitute the values of V and R into equation (i) as follows;
1.50 = I x 7710
I =
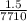
I = 0.00019A
Multiply the result by 1000 to convert it to milliamperes as follows;
0.00019 x 1000 mA = 0.19mA
Therefore, the initial current in the circuit, expressed in milliamperes is 0.19