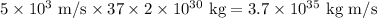Question

Two identical black holes collide head-on. Each of them has a mass equivalent to 37 solar masses. (The sun has a mass of about 2×1030 kg.) As the black holes collide, they merge, forming a single, larger black hole and additional gravitational waves that carry momentum out of the system. Before the collision, one black hole is moving with a speed of 56 km/s, while the other one is moving at 69 km/s. After the collision the larger black hole moves with speed 4 km/s. How much momentum was carried away by gravitational waves?

Answer 1

`3.7*10^(35)\text{ kg m/s}`

Step-by-step explanation:

The system of the colliding bodies is ideally isolated, so no external forces act on it. By the principle of conservation of linear momentum, the total initial momentum is equal to the total final momentum.

Both bodies had a head-on collision. We take the direction of the faster body as the positive direction. Because they have the same mass, let's call this mass m.

Hence, we have for the initial momentum

`69m - 56m = 13m`

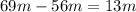
The final momentum is

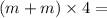`(m+m) *4 =`8m

The difference in both momenta is the momentum carried by the gravitational waves.

`13 m - 8m = 5m`

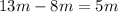
Converting to the appropriate units and using the actual value of m (37 × a solar mass), we have

`5*10^3 \text{ m/s}*37*2*10^(30) \text{ kg} = 3.7*10^(35)\text{ kg m/s}`