Question

A brochure claims that the average maximum height for a certain type of plant is 0.7 m. A gardener suspects that this is not accurate locally due to variation in soil conditions, and believes the local height is shorter. A random sample of 40 mature plants is taken. The mean height of the sample is 0.65 m with a standard deviation of 0.20 m. Test the claim that the local mean height is less than 0.7 m using a 5% level of significance.

Answer 1

As
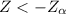`Z<-Z_(\alpha)`, it is possible to reject null hypotesis. It means that the local mean height is less tha 0.7 m with a 5% level of significance.

Explanation:

1. Relevant data:

`\mu=0.70\\N=40\\\alpha=0.05\\X=0.65\\s=0.20`

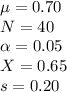
2. Hypotesis testing

`H_(0)=\mu=0.70`

`H_(1) =\mu< 0.70`

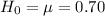
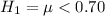
3. Find the rejection area

From the one tail standard normal chart, whe have Z-value for
`\alpha=0.05` is 1.56

Then rejection area is left 1.56 in normal curve.

4. Find the test statistic:

`Z=(X-\mu_(0) )/(\sigma/√(n))`

`Z=(0.65-0.70)/(0.20/√(40))\\Z=-1.58`

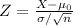
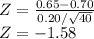
5. Hypotesis Testing

`Z_(\alpha)=1.56\\Z=-1.58`

`-1.58<-1.56`

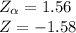
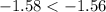
As
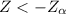`Z<-Z_(\alpha)`, it is possible to reject null hypotesis. It means that the local mean height is less tha 0.7 m with a 5% level of significance.