Answer:
Probability that glucose exceeds 120 in this population is 0.09012.
Explanation:
We are given that in a population of adults between the ages of 18 and 49, glucose follows a normal distribution with a mean of 93.5 and standard deviation of 19.8, i.e.;
 = 93.5 and
= 93.5 and
 = 19.8 .
= 19.8 .
Let X = amount of glucose i.e. X ~ N(
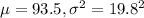 )
)
Now, the Z score probability is given by;
Z =
 ~ N(0,1)
~ N(0,1)
So,Probability that glucose exceeds 120 in this population =P(X>120)
P(X > 120) = P(
 >
>
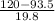 ) = P(Z > 1.34) = 1 - P(Z <= 1.34)
) = P(Z > 1.34) = 1 - P(Z <= 1.34)
= 1 - 0.90988 = 0.09012 .