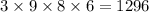Question

Use the fundamental counting principle to solve the problem. How many different codes of 4 digits are possible if the first digit must be​ 3, 4, or 5 and if the code may not end in​ 0?

Answer 1

Answer and Explanation:

Given,

4 digits and 10 digits.

Firstly, we have to find that when it repeats the digit then

• First position code would be filled in by Three methods that is 3, 4, or 5.
• Second position code would be filled in by Ten methods.
• Third position code would also be filled in by Ten methods.
• Fourth position code would be filled in by 9 way but 0 is rejected.
• So, the total numbers of methods in the following case is
  `3*10*10* 9=2700`.

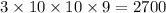Then, we have to find that when it not repeats the digit then

• First position code would be filled in by Three methods that is 3, 4, or 5.
• Second position code would be filled in by Nine methods in which one is reserved earlier.
• Third position code would be filled in by Eight methods in which two are reserved earlier.
• Fourth position code would be filled in by Six methods in which three are reserved earlier.
• So, the total numbers of methods in the following case is
  `3*9*8*6=1296`