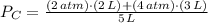Question

When the valve between the 2.00-L bulb, in which the gas pressure is 2.00 atm, and the 3.00-L bulb, in which the gas pressure is 4.00 atm, is opened, what will be the final pressure in the two bulbs

Answer 1

`P_(C) = 3.2\, atm`

Step-by-step explanation:

Let assume that gases inside bulbs behave as an ideal gas and have the same temperature. Then, conditions of gases before and after valve opened are now modelled:

Bulb A (2 L, 2 atm) - Before opening:

`P_(A) \cdot V_(A) = n_(A) \cdot R_(u) \cdot T`

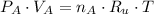
Bulb B (3 L, 4 atm) - Before opening:

`P_(B) \cdot V_(B) = n_(B) \cdot R_(u) \cdot T`

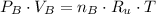
Bulbs A & B (5 L) - After opening:

`P_(C) \cdot (V_(A) + V_(B)) = (n_(A) + n_(B))\cdot R_(u) \cdot T`

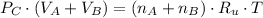
After some algebraic manipulation, a formula for final pressure is derived:

`P_(C) = (P_(A)\cdot V_(A) + P_(B)\cdot V_(B))/(V_(A)+V_(B))`

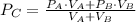
And final pressure is obtained:

`P_(C) = ((2\,atm)\cdot (2\,L)+(4\,atm)\cdot(3\,L))/(5\,L)`

`P_(C) = 3.2\, atm`