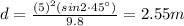Answer:
2.55 m
Step-by-step explanation:
The motion of the dancer is the motion of a projectile, which consists of 2 independent motions:
- A uniform motion (constant velocity) along the horizontal direction
- A uniformly accelerated motion (constant acceleration) along the vertical direction
The horizontal range of a projectile can be found by using the equations of motions along the two directions, and it is given by:
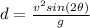
where
v is the intial velocity
 is the angle of projection
is the angle of projection
 is the acceleration due to gravity
is the acceleration due to gravity
For the dancer in this problem, we have:
v = 5 m/s
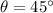
Therefore, the horizontal range is: