a)
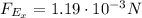 (+x axis)
(+x axis)
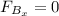
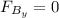
b)
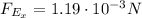 (+x axis)
(+x axis)
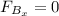
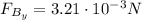 (+z axis)
(+z axis)
c)
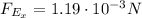 (+x axis)
(+x axis)
 (+y axis)
(+y axis)
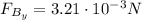 (-x axis)
(-x axis)
Step-by-step explanation:
a)
The electric force exerted on a charged particle is given by
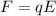
where
q is the charge
E is the electric field
For a positive charge, the direction of the force is the same as the electric field.
In this problem:
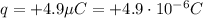 is the charge
is the charge
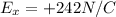 is the electric field, along the x-direction
is the electric field, along the x-direction
So the electric force (along the x-direction) is:
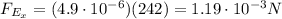
towards positive x-direction.
The magnetic force instead is given by
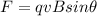
where
q is the charge
v is the velocity of the charge
B is the magnetic field
 is the angle between the directions of v and B
is the angle between the directions of v and B
Here the charge is stationary: this means
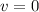 , therefore the magnetic force due to each component of the magnetic field is zero.
, therefore the magnetic force due to each component of the magnetic field is zero.
b)
In this case, the particle is moving along the +x axis.
The magnitude of the electric force does not depend on the speed: therefore, the electric force on the particle here is the same as in part a,
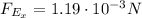 (towards positive x-direction)
(towards positive x-direction)
Concerning the magnetic force, we have to analyze the two different fields:
-
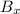 : this field is parallel to the velocity of the particle, which is moving along the +x axis. Therefore,
: this field is parallel to the velocity of the particle, which is moving along the +x axis. Therefore,
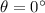 , so the force due to this field is zero.
, so the force due to this field is zero.
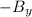 : this field is perpendicular to the velocity of the particle, which is moving along the +x axis. Therefore,
: this field is perpendicular to the velocity of the particle, which is moving along the +x axis. Therefore,
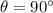 . Therefore,
. Therefore,
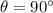 , so the force due to this field is:
, so the force due to this field is:
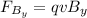
where:
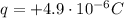 is the charge
is the charge
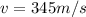 is the velocity
is the velocity
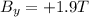 is the magnetic field
is the magnetic field
Substituting,
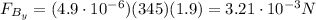
And the direction of this force can be found using the right-hand rule:
- Index finger: direction of the velocity (+x axis)
- Middle finger: direction of the magnetic field (+y axis)
- Thumb: direction of the force (+z axis)
c)
As in part b), the electric force has not change, since it does not depend on the veocity of the particle:
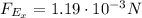 (+x axis)
(+x axis)
For the field
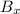 , the velocity (+z axis) is now perpendicular to the magnetic field (+x axis), so the force is
, the velocity (+z axis) is now perpendicular to the magnetic field (+x axis), so the force is
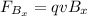
And by substituting,
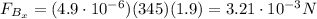
And by using the right-hand rule:
- Index finger: velocity (+z axis)
- Middle finger: magnetic field (+x axis)
- Thumb: force (+y axis)
For the field
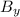 , the velocity (+z axis) is also perpendicular to the magnetic field (+y axis), so the force is
, the velocity (+z axis) is also perpendicular to the magnetic field (+y axis), so the force is
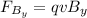
And by substituting,
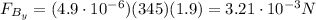
And by using the right-hand rule:
- Index finger: velocity (+z axis)
- Middle finger: magnetic field (+y axis)
- Thumb: force (-y axis)