Question

Sand falls from a conveyor belt at a rate of 30 m3m3/min onto the top of a conical pile. The height of the pile is always 3535 of the base diameter. Answer the following. a.) How fast is the height changing when the pile is 2 m high?

Answer 1

Step-by-step explanation:

As the given data is as follows.

h =
`(3)/(5)d`

=
`(3)/(5) * (2r)`

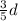
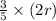
Also, we know that r =
`(4)/(3)h`

and Volume (V) =
`(1)/(3) \pir^(2)h`

=
`(1)/(3) \pi ((4)/(3)h)^(2) h`

=
`(16)/(27) \pi h^(3)`

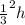
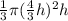
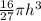
And,
`(dV)/(dt) = (3 * 16)/(27) \pi h^(2) (dh)/(dt)`

`(dV)/(dt) = (16)/(9) \pi h^(2) (dh)/(dt)`

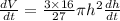
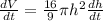
Putting the given values into the above formula as follows.

`(dV)/(dt) = (16)/(9) \pi h^(2) (dh)/(dt)`

`30 m^(3)/min = (16)/(9) \pi (2)^(2) (dh)/(dt)`

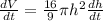
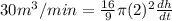
[tex]\frac{dh}{dt} = 1.343 m/min

or, = 134.3 cm/min (as 1 m = 100 cm)

thus, we can conclude that the height changing at 134.3 cm/min when the pile is 2 m high.