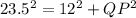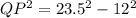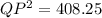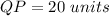Answer:
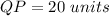
Explanation:
The picture of the question in the attached figure
Let
O ---> the center of the circle
we have that
Line segment QP is tangent to the circle
That means
OQ (radius) is perpendicular to segment QP
OQP is a right triangle
Applying Pythagorean Theorem
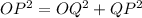
we have
The radius is equal to
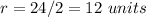 ----> the radius is half the diameter
----> the radius is half the diameter

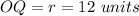
substitute