Question

Consider the titration of 50.0 mL of 1.00 M C5H5N by 0.500 M HCl. For each volume of HCl added, decide which of the components is a major species after the HCl has reacted completely. Kb for C5H5N

Answer 1

The given question is incomplete. The complete question is as follows.

Consider the titration of 50.0 mL of 1.00 M
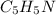`C_(5)H_(5)N` by 0.500 M HCl. For each volume of HCl added, decide which of the components is a major species after the HCl has reacted completely. Kb for
`C_(5)H_(5)N` =
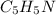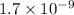`1.7 * 10^(-9)`. Calculate the pH at the equivalence point for this titration.

Step-by-step explanation:

Reaction equation of the given reaction is as follows.

`C_(5)H_(5)N + H^(+) \rightarrow C_(5)H_(5)NH^(+)`

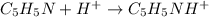
Only
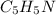`C_(5)H_(5)N` is present in the solution before the addition of HCl. Hence, the equation will be as follows.

`C_(5)H_(5)N + H_(2)O \overset{K_(b)}{\rightleftharpoons} C_(5)H_(5)NH^(+) + OH^(-)`

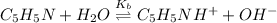
And, at the equivalence point entire
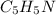`C_(5)H_(5)N` will completely react with the HCl. Hence, the solution contains
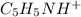`C_(5)H_(5)NH^(+)` at the equivalence point. It is acidic with a pH less than 7.

No. of moles of HCl = No. of moles of
`C_(5)H_(5)N`

`V_(HCl) * M_(HCl) = V_{C_(5)H_(5)N} * M_{C_(5)H_(5)N}`

`V_(HCl) * 0.5 M = 50 ml * 1 M`

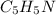
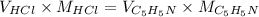
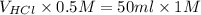
`V_(HCl)` = 100 ml

Hence, the volume of HCl at the equivalence point is 100 ml.

Also,
`k_(a) = (k_(w))/(k_(b))`

=
`(1 * 10^(-14))/(1.7 * 10^(-19))`

=
`5.9 * 10^(-6)`

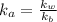
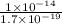
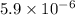
Therefore, concentration of the acid is calculated as follows.

Concentration =
`\frac{\text{No. of moles of acid}}{\text{Volume of solution}}`

=
`(0.05)/(0.15)`

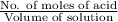
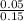
= 0.333 M

Since,
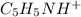`C_(5)H_(5)NH^(+)` is a weak acid. So,

`[H^(+)] = \sqrt{k_(a) * C}`

=
`\sqrt{5.9 * 10^(-6) * 0.333 M}`

=
`1.40 * 10^(-3)`

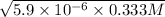
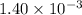
Now, we will calculate the pH of the solution at the equivalence point as follows.

pH =
`-log (1.40 * 10^(-3))`

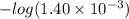
= 2.85

Thus, we can conclude that pH at the equivalence point for this titration is 2.85.