Question

Two balanced dice are rolled. Let X be the sum of the two dice. Obtain the probability distribution of X (i.e. what are the possible values for X and the probability for obtaining each value?). Check that the probabilities sum to one.

1) What is the probability for obtaining X \geq 8?

2) What is the average value of X?

Answer 1

Explanation:

Each die has faces numbered from 1 to 6. Hence, the sums range from 2 to 12.

There are 6 × 6 = 36 possible combinations of the dice.

The sums, their possible combinations and their probabiities are as below:

2 = 1+1 1/36

3 = 1+2 = 2+1 2/36= 1/18

4 = 1+3 = 2+2 = 3+1 3/36= 1/12

5 = 1+4 = 2+3 = 3+2 = 4+1 4/36= 1/9

6 = 1+5 = 2+4 = 3+3 = 4+2 = 5+1 5/36

7 = 1+6 = 2+5 = 3+4 = 4+3 = 5+2 = 6+1 6/36= 1/6

8 = 2+6 = 3+5 = 4+4 = 5+3 = 6+2 5/36

9 = 3+6 = 4+5 = 5+4 = 6+3 4/36= 1/9

10 = 4+6 = 5+5 = 6+4 3/96= 1/12

11 = 5+6 = 6+5 2/36= 1/18

12 = 6+6 1/36

Sum of probabilities = 1/36 + 1/18 + 1/12 + 1/9 + 5/36 + 1/6 + 5/36 + 1/9 + 1/12 + 1/18 + 1/36 = 1

1)
`P(X\ge 8) = 5/36+1/9+1/12+1/18+1/36=15/36`

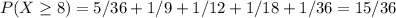
2) The average value of X = 1/36*(2+12) + 1/18*(3+11) + 1/12*(4+10)+ 1/9(5+9)+ 5/36(6+8)+ 1/6(7) = 14*(5/6)+7/6 = 77/6