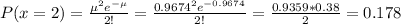Question

In analyzing hits by certain bombs in a​ war, an area was partitioned into 553 ​regions, each with an area of 0.95 km2. A total of 535 bombs hit the combined area of 553 regions. Assume that we want to find the probability that a randomly selected region had exactly two hits. In applying the Poisson probability distribution​ formula, ​P(x)equalsStartFraction mu Superscript x Baseline times e Superscript negative mu Over x exclamation mark EndFraction ​, identify the values of mu​, ​x, and e. ​Also, briefly describe what each of those symbols represents. Identify the values of mu​, ​x, and e.

Answer 1

Probability of having two hits in the same region = 0.178

mu: average number of hits per region

x: number of hits

e: mathematical constant approximately equal to 2.71828.

Explanation:

We can describe the probability of k events with the Poisson distribution, expressed as:

`P(x=k)=(\mu^ke^(-\mu))/(k!)`

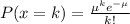
Being μ the expected rate of events.

If 535 bombs hit 553 regions, the expected rate of bombs per region (the events for this question) is:

`\mu=(\#bombs)/(\#regions) =(535)/(553)= 0.9674`

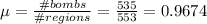
For a region to being hit by two bombs, it has a probability of:

`P(x=2)=(\mu^2e^(-\mu))/(2!)=(0.9674^2e^(-0.9674))/(2!)=(0.9359*0.38)/(2)=0.178`