Question

What are (a) the x component and (b) the y component of a vector in the xy plane if its direction is 259° counterclockwise from the positive direction of the x axis and its magnitude is 5.4 m?

Answer 1

(a) -1.030m

(b) -5.301m

Step-by-step explanation:

Given a vector F in the xy plane, of magnitude F and in a direction θ counterclockwise from the positive direction of the x-axis;

The x-component (
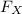`F_(X)`) of vector F is given by;

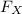`F_(X)` = F cos θ ---------------------(i)

And;

The y-component (
`F_(Y)`) of vector F is given by;

`F_(Y)` = F sin θ -----------------------(ii)

Now to the question;

Let the vector be A

Therefore;

The magnitude of vector A is A = 5.4m

The direction θ of A counterclockwise from the positive direction of the x-axis = 259°

(a) The x-component (
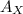`A_(X)`) of the vector A is therefore given by;

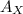`A_(X)` = A cos θ ------------------------(iii)

Substitute the values of θ and A into equation (iii) as follows;

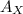`A_(X)` = 5.4 cos 259°

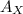`A_(X)` = 5.4 x (-0.1908)

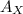`A_(X)` = -1.030

Therefore, the x-component of the vector is -1.030m

(b) The y-component (
`A_(Y)`) of the vector A is therefore given by;

`A_(Y)` = A sin θ ------------------------(iv)

Substitute the values of θ and A into equation (iv) as follows;

`A_(Y)` = 5.4 sin 259°

`A_(Y)` = 5.4 x (-0.9816)

`A_(Y)` = -5.301m

Therefore, the y-component of the vector is -5.301m

Answer 2

|Ax| =1.03 m (directed towards negative x-axis)

|Ay|= 5.30 (directed towards negative y-axis)

Step-by-step explanation:

Let A is a vector = 5.4 m

θ = 259°

to Find Ax, Ay

Sol:

according the condition it lies in 3rd quadrant

we know that Horizontal Component Ax = A cos θ

Ax = 5.4 Cos 259°

Ax = - 1.03 m

|Ax| =1.03 m (directed towards negative x-axis)

Now Ay = A sin θ

Ay = 5.4 Sin 259°

Ay = -5.30

|Ay|= 5.30 (directed towards negative y-axis)