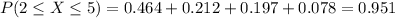Question

A family is selected at random from the city. Find the probability that the size of the family is between 2 and 5 inclusive. Round approximations to three decimal places.

Answer 1

`P(2 \leq X \leq 5)`

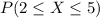
And using the table from the info we got:

`P(2 \leq X \leq 5) = P(X=2) +P(X=3) +P(X=4)+P(X=5)`

And replacing we got:

`P(2 \leq X \leq 5) =0.464+0.212+0.197+0.078= 0.951`

Explanation:

For this case we assume that following table shows the distribution of family size in a certain U.S. city

Family Size Probability

2 0.464

3 0.212

4 0.197

5 0.078

6 0.030

7+ 0.019

We assume that X represent the random variable "family size"

And for this case we want to find this probability:

`P(2 \leq X \leq 5)`

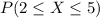
And using the table from the info we got:

`P(2 \leq X \leq 5) = P(X=2) +P(X=3) +P(X=4)+P(X=5)`

And replacing we got:

`P(2 \leq X \leq 5) =0.464+0.212+0.197+0.078= 0.951`