Answer:
The answer to the question is
The longest interval in which the given initial value problem is certain to have a unique twice-differentiable solution is (-∞, 4)
Explanation:
To apply look for the interval, we divide the ordinary differential equation by (t-4) to
y'' +
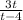 y' +
y' +
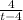 y =
y =
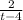
Using theorem 3.2.1 we have p(t) =
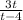 , q(t) =
, q(t) =
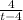 , g(t) =
, g(t) =
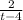
Which are undefined at 4. Therefore the longest interval in which the given initial value problem is certain to have a unique twice-differentiable solution, that is where p, q and g are continuous and defined is (-∞, 4) whereby theorem 3.2.1 guarantees unique solution satisfying the initial value problem in this interval.