Complete Question:
A fatigue test was conducted in which the mean stress was 50 MPa (7,250 psi) and the stress amplitude was 225 MPa (32,625 psi).
(a) Compute the maximum and minimum stress levels.
(b) Compute the stress ratio.
(c) Compute the magnitude of the stress range.
Answer:
(a) The maximum and minimum stress levels are 275MPa and -175MPa respectively.
(b) The stress ratio is 0.6
(c) The magnitude of the stress range is 450MPa
Step-by-step explanation:
(a )In fatigue, the mean stress (
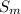 ) is found by finding half of the sum of the maximum stress (
) is found by finding half of the sum of the maximum stress (
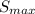 ) and minimum stress (
) and minimum stress (
 ) levels. i.e
) levels. i.e
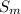 =
=
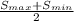 ------------------------(i)
------------------------(i)
Also, the stress amplitude (also called the alternating stress),
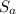 , is found by finding half of the difference between the maximum stress (
, is found by finding half of the difference between the maximum stress (
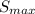 ) and minimum stress (
) and minimum stress (
 ) levels. i.e
) levels. i.e
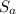 =
=
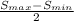 ------------------------(ii)
------------------------(ii)
From the question,
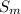 = 50 MPa (7250 psi)
= 50 MPa (7250 psi)
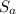 = 225 MPa (32,625 psi)
= 225 MPa (32,625 psi)
Substitute these values into equations(i) and (ii) as follows;
50 =
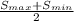
=> 100 =
 +
+
 -------------------(iii)
-------------------(iii)
225 =
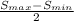
=> 450 =
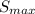 -
-
 -------------------(iv)
-------------------(iv)
Now, solve equations (iii) and (iv) simultaneously as follows;
(1) add the two equations;
100 =
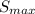 +
+

450 =
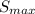 -
-

________________
550 = 2
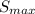 --------------------------------(v)
--------------------------------(v)
_________________
(2) Divide both sides of equation (v) by 2 as follows;
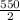 =
=
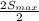
275 =
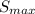
Therefore, the maximum stress level is 275MPa
(3) Substitute
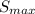 = 275 into equation (iv) as follows;
= 275 into equation (iv) as follows;
450 = 275 -

 = 275 - 450
= 275 - 450
 = -175
= -175
Therefore, the minimum stress level is -175MPa
In conclusion, the maximum and minimum stress levels are 275MPa and -175MPa respectively.
===============================================================
(b) The stress ratio (
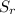 ) is given by;
) is given by;
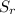 =
=
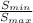 ----------------------------(vi)
----------------------------(vi)
Insert the values of
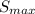 and
and
 into equation (vi)
into equation (vi)
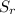 =
=
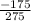
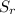 = 0.6
= 0.6
Therefore, the stress ratio is 0.6
===============================================================
(c) The magnitude of the stress range (
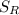 ) is given by
) is given by
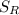 = |
= |
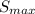 -
-
 | ------------------------------(vii)
| ------------------------------(vii)
Insert the values of
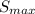 and
and
 into equation (vii)
into equation (vii)
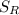 = | 275 - (-175) |
= | 275 - (-175) |
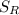 = 450MPa
= 450MPa
Therefore, the magnitude of the stress range is 450MPa
===============================================================
Note:
1 MPa = 145.038psi
Therefore, the values of the maximum and minimum stress levels, the stress range can all be converted from MPa to psi (pounds per inch square) by multiplying the values by 145.038 as follows;
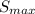 = 275MPa = 275 x 145.038psi = 39885.45psi
= 275MPa = 275 x 145.038psi = 39885.45psi
 = -175MPa = -175 x 145.038psi = 25381.65psi
= -175MPa = -175 x 145.038psi = 25381.65psi
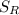 = 450MPa = 450 x 145.038psi = 65267.1psi
= 450MPa = 450 x 145.038psi = 65267.1psi