Here is the full question:
Air containing 0.04% carbon dioxide is pumped into a room whose volume is 6000 ft3. The air is pumped in at a rate of 2000 ft3/min, and the circulated air is then pumped out at the same rate. If there is an initial concentration of 0.2% carbon dioxide, determine the subsequent amount in the room at any time.
What is the concentration at 10 minutes? (Round your answer to three decimal places.
Answer:
0.046 %
Step-by-step explanation:
The rate-in;
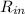

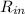 = 0.8
= 0.8
The rate-out
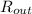 =
=
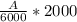
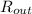 =
=
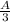
We can say that:
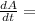
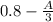
where;
A(0)= 0.2% × 6000
A(0)= 0.002 × 6000
A(0)= 12
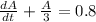
Integration of the above linear equation =
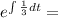
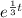
so we have:
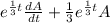
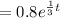
![(d)/(dt)[e^{(1)/(3)t}A]](https://img.qammunity.org/2021/formulas/chemistry/high-school/mxb316l9ucj29pphv4s51gp54ivvemx96f.png)
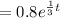
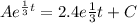
∴

Since A(0) = 12
Then;
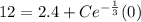
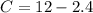
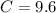
Hence;

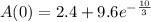
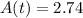
∴ the concentration at 10 minutes is ;
=
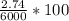 %
%
= 0.0456667 %
= 0.046% to three decimal places