Question

A spotlight on a boat is y = 2.2 m above the water, and the light strikes the water at a point that is x = 8.5 m horizontally displaced from the spotlight (see the drawing). The depth of the water is 4.0 m. Determine the distance d, which locates the point where the light strikes the bottom.

Answer 1

The answer to the question is

The distance d, which locates the point where the light strikes the bottom is 29.345 m from the spotlight.

Step-by-step explanation:

To solve the question we note that Snell's law states that

The product of the incident index and the sine of the angle of incident is equal to the product of the refractive index and the sine of the angle of refraction

n₁sinθ₁ = n₂sinθ₂

y = 2.2 m and strikes at x = 8.5 m, therefore tanθ₁ = 2.2/8.5 = 0.259 and

θ₁ = 14.511 °

n₁ = 1.0003 = refractive index of air

n₂ = 1.33 = refractive index of water

Therefore sinθ₂ =
`(n_1sin\theta_1)/(n_2)` =
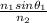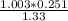`(1.003*0.251)/(1.33)` = 0.1885 and θ₂ = 10.86 °

Since the water depth is 4.0 m we have tanθ₂ =
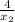`(4)/(x_2)` or x₂ =
`(4)/(tan\theta_2 )` =
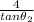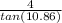`(4)/(tan(10.86))` = 20.845 m

d = x₂ + 8.5 = 20.845 m + 8.5 m = 29.345 m.