Question

A linear accelerator produces a pulsed beam of electrons. The pulse current is 0.50 A, and the pulse duration is 0.10 μs. (a) How many electrons are accelerated per pulse? (b) What is the average current for a machine operating at 500 pulses/s? If the electrons are accelerated to an energy of 50 MeV, what are the (c) average power and (d) peak power of the accelerator?

Answer 1

Step-by-step explanation:

Below is an attachment containing the solution.

Answer 2

a)N = 3.125 * 10¹¹

b) I(avg) = 2.5 × 10⁻⁵A

c)P(avg) = 1250W

d)P = 2.5 × 10⁷W

Step-by-step explanation:

Given that,

pulse current is 0.50 A

duration of pulse Δt = 0.1 × 10⁻⁶s

a) The number of particles equal to the amount of charge in a single pulse divided by the charge of a single particles

N = Δq/e

charge is given by Δq = IΔt

so,

N = IΔt / e

`N = ((0.5)(0.1 * 10^-^6))/((1.6 * 10^-^1^9)) \\= 3.125 * 10^1^1`

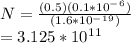
N = 3.125 * 10¹¹

b) Q = nqt

where q is the charge of 1puse

n = number of pulse

the average current is given as I(avg) = Q/t

I(avg) = nq

I(avg) = nIΔt

= (500)(0.5)(0.1 × 10⁻⁶)

= 2.5 × 10⁻⁵A

C) If the electrons are accelerated to an energy of 50 MeV, the acceleration voltage must,

eV = K

V = K/e

the power is given by

P = IV

P(avg) = I(avg)K / e

`P(avg) = ((2.5 * 10^-^5)(50 * 10^6 . 1.6 * 10^-^1^9))/(1.6 * 10^-^1^9)`

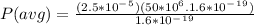
= 1250W

d) Final peak=

P= Ik/e

=
`= P(avg) = ((0.5)(50 * 10^6 . 1.6 * 10^-^1^9))/(1.6 * 10^-^1^9)\\2.5 * 10^7W`

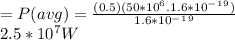
P = 2.5 × 10⁷W