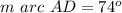2 Answers

Oleksiy · Answer 1 · 2021-10-30T16:26:02+0000

Answer:

74°

Explanation:

see the attached figure to better understand the problem

we know that

Triangle EBC is an isosceles triangle (because has two equal sides EB=EC)

so

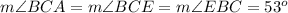
$m\angle BCA=m\angle BCE=m\angle EBC=53^o$

Find the measure of angle BEC

Remember that the sum of the interior angles in any triangle must be equal to 180 degrees

so

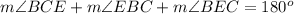
$m\angle BCE+m\angle EBC+m\angle BEC=180^o$

substitute the given values

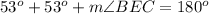
$53^o+53^o+m\angle BEC=180^o$

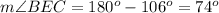
$m\angle BEC=180^o-106^o=74^o$

Find the measure of angle AED

we know that

$m\angle AED=m\angle BEC$ ----> by vertical angles

so

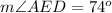
$m\angle AED=74^o$

Find the measure of arc AD

we know that

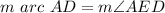$m\ arc\ AD=m\angle AED$ -----> by central angle

therefore

$m\ arc\ AD=74^o$

Please log in or register to add a comment.