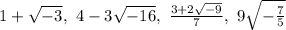The complex number from the table are
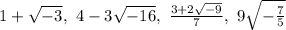
Solution:
Let us solve and identify the complex number.
(A)
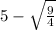
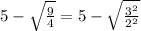

= 3.5
This is not a complex number.
(B)
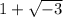
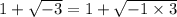
We know that
 .
.
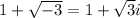
This is a complex number.
(C)
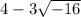
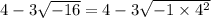
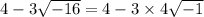
We know that
 .
.
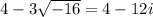
This is a complex number.
(D)
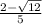
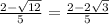
There is no –1 in the root.
This is not a complex number.
(E)
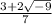
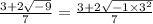
We know that
 .
.
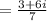
This is a complex number.
(F)
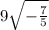
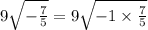
We know that
 .
.
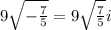
This is a complex number.
Hence the complex number from the table are