Answer:
The random variable X follows a Binomial distribution.

Explanation:
The random variable X defined as the number of children who have been diagnosed with ASD.
The random sample of children selected is of size n = 300.
The probability of children diagnosed with ASD is,
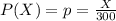 .
.
A children diagnosed with ASD is independent of all the others.
The random variable X follows a Binomial distribution.
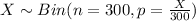
The expected value of X is:
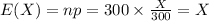
The standard deviation of X is:
![SD(X)=√(np(1-p))=\sqrt{300* (X)/(300)[1-(X)/(300)]}=\sqrt{(X(300-X))/(300)}](https://img.qammunity.org/2021/formulas/mathematics/high-school/6sj7ll76cznab2vlpoqfs78xg3ayfrli8q.png)