Step-by-step explanation:
It is known that,
No. of moles = Molarity × Volume
So, we will calculate the moles of
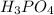 as follows.
as follows.
No. of moles =
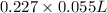
= 0.0125 mol
Now, the moles of KOH are as follows.
No. of moles =

= 0.0374 mol
And,
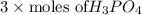 =
=
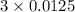
= 0.0375 mol
Now, the balanced reaction equation is as follows.

This means 1 mole of
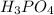 produces 173.2 kJ of heat. And, the amount of heat produced by 0.0125 moles of
produces 173.2 kJ of heat. And, the amount of heat produced by 0.0125 moles of
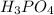 is as follows.
is as follows.
M =
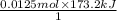
= 2.165 kJ
Total volume of the solution = (55.0 + 55.0) ml
= 110 ml
Density of the solution = 1.13 g/ml
Mass of the solution = Volume × Density
=
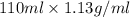
= 124.3 g
Specific heat = 3.78
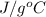
Now, we will calculate the final temperature as follows.
q =

2165 J =
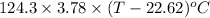
2165 - 469.854 =
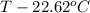
17.417 =
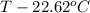
T =

Thus, we can conclude that final temperature of the solution is
 .
.