Question

A tugboat tows a ship with a constant force of magnitude F1. The increase in the ship's speed during a 10 s interval is 3.0 km/h. When a second tugboat applies an additional constant force of magnitude F2 in the same direction, the speed increases by 11 km/h during a 10 s interval. How do the magnitudes of F1 and F2 compare? (Neglect the effects of water resistance and air resistance.)

Answer 1

The magnitude of F₁ is 3.7 times of F₂

Step-by-step explanation:

Given that,

Time = 10 sec

Speed = 3.0 km/h

Speed of second tugboat = 11 km/h

We need to calculate the speed

`v_(1)=(3.0*10^(3))/(3600)`

`v_(1)=0.833\ m/s`

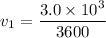
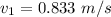
The force F₁is constant acceleration is also a constant.

`F_(1)=ma_(1)`

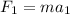
We need to calculate the acceleration

Using formula of acceleration

`a_(1)=(v)/(t)`

`a_(1)=(0.833)/(10)`

`a_(1)=0.083\ m/s^2`

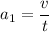
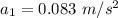
Similarly,

`F_(2)=ma_(2)`

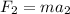
For total force,

`F_(3)=F_(2)+F_(1)`

`ma_(3)=ma_(2)+ma_(1)`

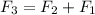
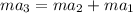
The speed of second tugboat is

`v=(11*10^(3))/(3600)`

`v=3.05\ m/s`

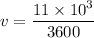
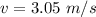
We need to calculate total acceleration

`a_(3)=(v)/(t)`

`a_(3)=(3.05)/(10)`

`a_(3)=0.305\ m/s^2`

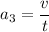
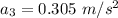
We need to calculate the acceleration a₂

`0.305=a_(2)+0.083`

`a_(2)=0.305-0.083`

`a_(2)=0.222\ m/s^2`

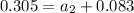
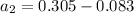
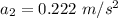
We need to calculate the factor of F₁ and F₂

Dividing force F₁ by F₂

`(F_(1))/(F_(2))=(m*0.83)/(m*0.22)`

`(F_(1))/(F_(2))=3.7`

`F_(1)=3.7F_(2)`

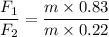
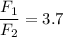
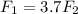
Hence, The magnitude of F₁ is 3.7 times of F₂