Question

What is the frequency of the function f(x)?

f(x)=−sin(3x)−1




Enter your answer, in simplest fraction form, in the box.

Answer 1

F=3

Explanation:

Due to the difficulty of visualizing the graph of the function in degrees (graph 1), we will graph it in radians (graph 2)

f(x)=−sin(3x)−1 ≡ y=−sin(3x)−1

To graph y=−sin(3x)−1

y=a.sin(bx+c)+d, where

a=-1, b=3, c=0, d=-1 and the period (T) of the function is:

`T=(2\pi )/(b)=(2\pi )/(3)`

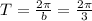
On the graph 2 we place the original function y=sin(x) to compare

We watch that y=−sin(3x)−1 moves 1 down (-), but amplitud is the same (1)

Frequency is the number of repetitions (3x) of a function in a given interval, so

F=3