Question

How did the graph of f(x) = x^2 and g(x) = 3/4 x^2 relate?

Answer 1

g(x) =
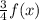`(3)/(4) f(x)` or g(x) is 3/4 times of f(x) , F(x) and g(x) have common solution or intersecting point in the graph parabola at x=0 i.e. in origin and x =
`\frac {4}{3}`.

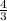Explanation:

We have a function f(x) =
`x^(2)` and another function , g(x) =
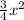`(3)/(4) x^(2)`. In the graph of y =
`x^(2)` , the point (0, 0) is called the vertex. The vertex is the minimum point in a parabola that opens upward. In a parabola that opens downward, the vertex is the maximum point.

Graphing y = (x - h)2 + k , where h = 0 & k = 0

Function g(x) can be formed with compression in function f(x) by a factor of 3/4 , i.e. g(x) =
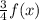`(3)/(4) f(x)` or g(x) is 3/4 times of f(x).Domain and range of f(x) and g(x) are same ! Although structure of both functions is same the only difference is g(x) is compressed vertically by a factor 3/4. Both are graph of a parabola with vertex at (0,0). Also, F(x) and g(x) have common solution or intersecting point at x=0 i.e. in origin.