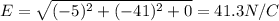Answer:
a)
The expression for the electric potential in this problem is:

where
x, y, z are the three spatial coordinates
The relationship between components of the electric field and electric potential is:
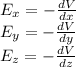
Therefore, we have to calculate the derivatives of the potential over the three variables.
Doing so, we find:
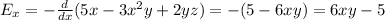
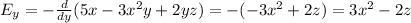
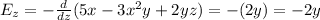
b)
Here we want to find the magnitude of the electric field at the point P that has coordinates
P (1.00, 0, 22.00) m
First of all, we find the components of the electric field at that point by substituting
x = 1.00
y = 0
z = 22.0
We find:

Now, the magnitude of the electric field is given by
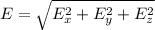
And by substituting,