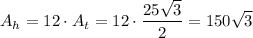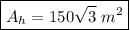Question

Use the rectangle hexagon with side length 10 meters to fill in the missing information

Answer 1

`A_h=150√(3)\ m^2`

Explanation:

Regular Hexagon

For the explanation of the answer, please refer to the image below. Let's analyze the triangle shown inside of the hexagon. It's a right triangle with sides x,y, and z.

We know that x is half the length of the side length of the hexagon. Thus

`x=5 m`

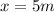
Note that this triangle repeats itself 12 times into the shape of the hexagon. The internal angle of the triangle is one-twelfth of the complete rotation angle, i.e.

`\theta=360/12=30^o`

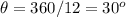
Now we have
`\theta`, the height of the triangle y is easily found by

`\displaystyle tan30^o=(x)/(y)`

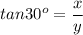
Solving for y

`\displaystyle y=(x)/(tan30^o)=\frac{5}{ \frac{1} {√(3) }}=5√(3)`

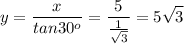
The value of z can be found by using

`\displaystyle sin30^o=(x)/(z)`

`\displaystyle z=(x)/(sin30^o)=(5)/((1)/(2))=10`

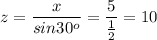
The area of the triangle is

`\displaystyle A_t=(xy)/(2)=(5\cdot 5√(3))/(2)=(25√(3))/(2)`

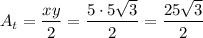
The area of the hexagon is 12 times the area of the triangle, thus

`\displaystyle A_h=12\cdot A_t=12\cdot (25√(3))/(2)=150√(3)`

`\boxed{A_h=150√(3)\ m^2}`