The horizontal distance the plan has covered when it has flown 4,000 feet is 694 feet.
Explanation:
Step 1:
For the given triangle, assume the opposite side has a length of x units, the hypotenuse of the triangle measures 4,000 feet. The given angle of the triangle is 10°. To calculate the opposite side's length of the triangle, we use the sine of the given angle.
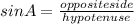
Step 2:
The length of the opposite side = x feet.
The length of the hypotenuse side = 4,500 feet.
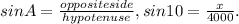
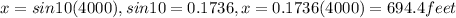 .
.
So the horizontal distance is 694.4 feet, rounding this off to the nearest foot, we get the horizontal distance as 694 feet.