Question

In a club there is 13 women and 8 men. A committee of 9 women and 4 men is to be chosen. How many different ways are there to select the committee?

A. 50,050 ways
B. 3,744 ways
C. 273 ways
D. 34 ways​

Answer 1

The total number of ways to select 9 women and 4 men for the committee is 50,050.

Explanation:

The club has 13 female members and 8 male members.

The committee to be formed must have 9 female members and 4 male members.

The possible number of ways to select 9 female from 13 females is:

`n(F)={13\choose 9}=(13!)/(9!(13-9)!)=715`

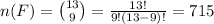
The possible number of ways to select 4 male from 8 males is:

`n(M)={8\choose 4}=(8!)/(4!(8-4)!)=70`

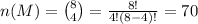
Compute the possible total number of ways to select 9 women and 4 men for the committee as follows:

Total number of ways to select 9 women and 4 men = n (F) × n (M)

`=715*70\\=50050`

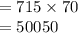
Thus, the total number of ways to select 9 women and 4 men for the committee is 50,050.