Question

Find the vertex and axis of symmetry for f(x)=2x^2-1

Answer 1

Axis of symmetry is 0 and vertex is (0, -1)

Solution:

Given is:

`f(x) = 2x^2 - 1`

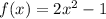
We have to find the vertex and axis of symmetry

The general equation is given as:

`f(x) = ax^2 + bx + c`

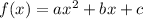
Comparing with given equation,

a = 2

b = 0

c = -1

The axis of symmetry is given as:

`x = (-b)/(2a)`

`x = (0)/(2(2))\\\\x = 0`

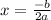
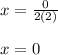
Thus axis of symmetry is 0

The x coordinate of the vertex is the same

x coordinate of the vertex = 0

h = 0

The y coordinate of the vertex is:

k = f(h)

k = f(0)

`f(0) = 2(0) - 1\\\\f(0) = 0 - 1\\\\f(0) = -1`

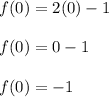
Thus, y coordinate of the vertex is -1

Therefore, vertex is (0, -1)