Axis of symmetry is 0 and vertex is (0, -1)
Solution:
Given is:
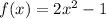
We have to find the vertex and axis of symmetry
The general equation is given as:
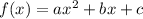
Comparing with given equation,
a = 2
b = 0
c = -1
The axis of symmetry is given as:
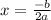
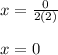
Thus axis of symmetry is 0
The x coordinate of the vertex is the same
x coordinate of the vertex = 0
h = 0
The y coordinate of the vertex is:
k = f(h)
k = f(0)
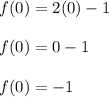
Thus, y coordinate of the vertex is -1
Therefore, vertex is (0, -1)