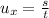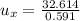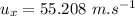Question

You are watching people practicing archery when you wonder how fast an arrow is shot from a bow. With a flash of insight you remember your physics and see how you can easily determine what you want to know by a simple measurement. You ask one of the archers to pull back her bow string as far as possible and shoot an arrow horizontally. The arrow strikes the ground 107 feet from the archer making an angle of 3 degrees below the horizontal. What is the initial speed of the arrow?

Answer 1

`u_x=55.208\ m.s^(-1)`

Step-by-step explanation:

Given:

horizontal distance form the point of shooting where the arrow hits ground,
`s=107\ ft`
`=32.614\ m`

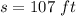
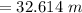
angle below the horizontal form the point of release of arrow where it hits ground,
`\theta=3^(\circ)`

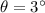
So the height above the ground from where the arrow was shot:

`\tan3^(\circ)=(h)/(107)`

`h=5.6076\ ft=1.71\ m`

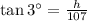
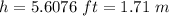
• Since the arrow is shot horizontally so the initial vertical component of the velocity is zero (
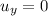  `u_y=0` ), we've the final vertical component of the velocity as:

`v_y=√(2g.h)`

`v_y=√(2* 9.8* 1.71)`

`v_y=5.789\ m.s^(-1)`

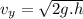
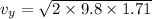
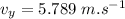
Using equation of motion:

`v_y=u_y+g.t`

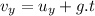
where:

t = time taken

`5.789=0+9.8* t`

`t=0.591\ s`

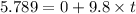
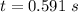
• Now the horizontal component of speed of the arrow (which remains constant throughout the motion by the Newton's first law of motion):

`u_x=(s)/(t)`

`u_x=(32.614)/(0.591)`

`u_x=55.208\ m.s^(-1)`