Question

√2

4
Suppose that $2000 is invested at a rate of 5.1%, compounded semiannually. Assuming that no withdrawals are made, find the total amount after 6 years.
Do not round any intermediate computations, and round your answer to the nearest cent.

Answer 1

The total amount after 6 years is $ 2705.5649

Solution:

The formula for compound interest, including principal sum, is:

`A = p( 1 + (r)/(n))^(nt)`

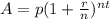
Where,

A = the future value of the investment/loan

P = the principal investment amount

r = the annual interest rate (decimal)

n = the number of times that interest is compounded per unit t

t = the time the money is invested

From given,

p = 2000

`r = 5.1 \% = (5.1)/(100) = 0.051`

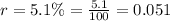
t = 6 years

n = 2 ( compounded semiannually)

Substituting the values we get,

`A = 2000( 1 + (0.051)/(2))^( 2 * 6)\\\\A = 2000( 1 + 0.0255)^(12)\\\\\A = 2000(1.0255)^(12)\\\\A = 2000 * 1.35278\\\\A = 2705.5649`

Thus the total amount after 6 years is $ 2705.5649