Answer:
26.06°
Step-by-step explanation:
Given an RLC circuit [a circuit containing a capacitor, inductor and resistor], the phase angle (Φ), which is the difference in phase between the voltage and the current in the circuit, is given by;
Φ = tan⁻¹ [
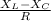 ] --------------------------(i)
] --------------------------(i)
Where;
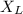 = inductive reactance of the circuit
= inductive reactance of the circuit
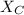 = capacitive reactance of the circuit
= capacitive reactance of the circuit
R = resistance of the circuit
From the question;
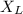 = 16.5 Ω
= 16.5 Ω
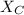 = 9.41 Ω
= 9.41 Ω
R = 14.5 Ω
Substitute these values into equation (i) as follows;
Φ = tan⁻¹ [
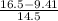 ]
]
Φ = tan⁻¹ [
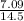 ]
]
Φ = tan⁻¹ [ 0.4890]
Φ = 26.06°
Therefore the phase angle of the AC series circuit is 26.06°