Answer:
Explanation:
Given that the owner of a motel has 2900 m of fencing and wants to enclose a rectangular plot of land that borders a straight highway.
Fencing is used for 2times length and 1 width if highway side is taken as width
So we have 2l+w = 2900
Or w = 2900-2l
Area of the rectangular region = lw

Use derivative test to find the maximum
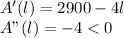
So maximum when I derivative =0
i.e when

Largest area = A(725)
=
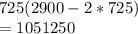
1051250 sqm is area maximum