Question

A mine is for sale for $800,000. It is believed the mine will produce a profit of $250,000 the first year, but the profit will decline $25,000 a year after that, eventually reaching zero, whereupon the mine will be worthless. What rate of return would be earned on the mine

Answer 1

`r=-60.8\%`

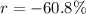
Step-by-step explanation:

Rate of Return

The rate of return RoR is the net gain or loss on an investment over a time period, expressed as a percentage of the investment's initial cost.

If C1, C2, ..., Cn are the net cash flows at each period of investment, then the actual value of each one of them is

`A_i=C_i(1+r)^(-i)`

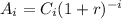
where r is the rate of interest assumed for the investment.

The total value of the cash flows is

`A=\sum C_i(1+r)^(-i)`

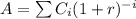
We have the final value of the investment at the present time

`A=800,000\ ;\ C_1=250,000\ ;\ C_2=25,000`

We can find the r as the RoR of the investment by setting the equation

`800,000=250,000(1+r)^(-1)+25,000(1+r)^(-2)`

Simplifying by 25,000 and rearranging

`(1+r)^(-2)+10(1+r)^(-1)-32=0`

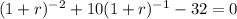
This is a second-degree equation for
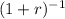`(1+r)^(-1)`. Solving the equation we get only one positive value:

`(1+r)^(-1)=2.5498`

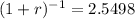
Or, equivalently

`r=-0.608`

`r=-60.8\%`

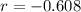
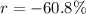
We get a negative RoR