Answer:
a) 9.52% probability that, in a year, there will be 4 hurricanes.
b) 4.284 years are expected to have 4 hurricanes.
c) The value of 4 is very close to the expected value of 4.284, so the Poisson distribution works well here.
Explanation:
In a Poisson distribution, the probability that X represents the number of successes of a random variable is given by the following formula:

In which
x is the number of sucesses
e = 2.71828 is the Euler number
 is the mean in the given time interval.
is the mean in the given time interval.
6.9 per year.
This means that

a. Find the probability that, in a year, there will be 4 hurricanes.
This is P(X = 4).
So

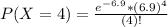
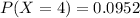
9.52% probability that, in a year, there will be 4 hurricanes.
b. In a 45-year period, how many years are expected to have 4 hurricanes?
For each year, the probability is 0.0952.
Multiplying by 45
45*0.0952 = 4.284.
4.284 years are expected to have 4 hurricanes.
c. How does the result from part (b) compare to a recent period of 45 years in which 4 years had 4 hurricanes? Does the Poisson distribution work well here?
The value of 4 is very close to the expected value of 4.284, so the Poisson distribution works well here.