Question

When a metal rod is heated, its resistance changes both because of a change in resistivity and because of a change in the length of the rod. If a silver rod has a resistance of 1.70 Ω at 21.0°C, what is its resistance when it is heated to 180.0°C? The temperature coefficient for silver is α = 6.1 ✕ 10−3 °C−1, and its coefficient of linear expansion is 18 ✕ 10−6 °C−1. Assume that the rod expands in all three dimensions.

Answer 1

`3.34\Omega`

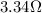
Step-by-step explanation:

The resistance of a metal rod is given by

`R=(\rho L)/(A)`

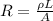
where

`\rho` is the resistivity

L is the length of the rod

A is the cross-sectional area

The resistivity changes with the temperature as:

`\rho(T)=\rho_0 (1+\alpha (T-T_0))`

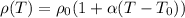
where in this case:

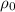`\rho_0` is the resistivity of silver at
`T_0=21.0^(\circ)C`

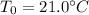
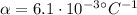`\alpha=6.1\cdot 10^(-3) ^(\circ)C^(-1)` is the temperature coefficient for silver

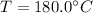`T=180.0^(\circ)C` is the current temperature

Substituting,

`\rho(180^(\circ)C)=\rho_0 (1+6.1\cdot 10^(-3)(180-21))=1.970\rho_0`

The length of the rod changes as

`L(T)=L_0 (1+\alpha_L(T-T_0))`

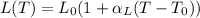
where:

`L_0` is the initial length at
`21.0^(\circ)C`

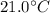
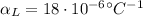`\alpha_L = 18\cdot 10^(-6) ^(\circ)C^(-1)` is the coefficient of linear expansion

Substituting,

`L(180^(\circ)C)=L_0(1+18\cdot 10^(-6)(180-21))=1.00286L_0`

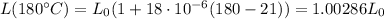
The cross-sectional area of the rod changes as

`A(T)=A_0(1+2\alpha_L(T-T_0))`

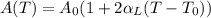
So, substituting,

`A(180^(\circ)C)=A_0(1+2\cdot 18\cdot 10^(-6)(180-21))=1.00572A_0`

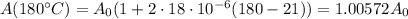
Therefore, if the initial resistance at 21.0°C is

`R_0 = (\rho_0 L_0)/(A_0)=1.70\Omega`

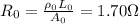
Then the resistance at 180.0°C is:

`R(180^(\circ)C)=(\rho(180)L(180))/(A(180))=((1.970\rho_0)(1.00285L_0))/(1.00572A_0)=1.9644(\rho_0 L_0)/(A_0)=1.9644 R_0=\\=(1.9644)(1.70\Omega)=3.34\Omega`