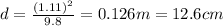a)
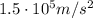
b) 6.3 cm
c) 12.6 cm
Step-by-step explanation:
a)
The acceleration of an object is the rate of change of its velocity; it is given by:
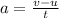
where
u is the initial velocity
v is the final velocity
t is the time interval taken for the velocity to change from u to t
In this problem for the spore, we have:
u = 0 (the spore starts from rest)
v = 1.11 m/s (final velocity of the spore)
 (time interval in which the spore accelerates from zero to 1.11 m/s)
(time interval in which the spore accelerates from zero to 1.11 m/s)
Substituting, we find the acceleration:
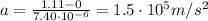
b)
Since the upward motion of the spore is a free fall motion (it is subjected to the force of gravity only), it is a uniformly accelerated motion (=constant acceleration, equal to the acceleration due to gravity:
 ). Therefore, we can apply the following suvat equation:
). Therefore, we can apply the following suvat equation:

where:
v = 0 is the final velocity of the spore (when it reaches the maximum height, its velocity is zero)
u = 1.11 m/s is the initial velocity (the velocity at which it is ejected)
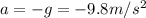 is the acceleration (negative because it is downward)
is the acceleration (negative because it is downward)
s is the vertical displacement of the spore, which corresponds to the maximum height reached by the spore
Solving for s, we find:
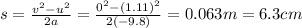
c)
If the spore is ejected at a certain angle
 from the ground, then its motion is a projectile motion, which consists of two independent motions:
from the ground, then its motion is a projectile motion, which consists of two independent motions:
- A uniform horizontal motion, with constant horizontal velocity
- A uniformly accelerated motion along the vertical direction (free fall motion)
The horizontal range of a projectile, which can be derived from the equations of motion, is given by:
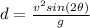
where
v is the initial velocity
 is the angle or projection
is the angle or projection
g is the acceleration of gravity
From the equation, we observe that the maximum range is achevied when
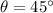
For this angle, the range is
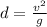
For the spore in this problem, the initial velocity is
v = 1.11 m/s
Therefore, the maximum range is