Option C:
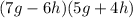 is the correct answer.
is the correct answer.
Step-by-step explanation:
The given expression is
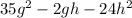
We need to determine the factor of the expression.
Now, let us break the given expression into two groups.
Hence, we get,
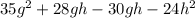
Simplifying, we get,
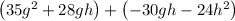
Let us factor out 7g from the term
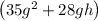
Hence, we have,
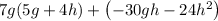
Similarly, let us factor out -6h from the term
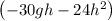
Thus, we have,

Now, we shall factor out the term
 , we get,
, we get,
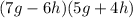
Thus, the factorization of the given expression is
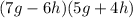
Therefore, Option C is the correct answer.