Answer:
t=11 sec
Explanation:
The position of the particle moving along the x-axis is given by:

The velocity is given by:
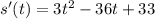
If s'(t)>0 then the particle is moving right.
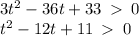
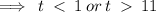
This means that the particle is moving left when

The particle changes direction at time t=1 or t=11