Question

Do y’all the answer?

Answer 1

Length = 12 m and width =
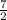`(7)/(2)` m.

Solution:

Let the width of the rectangle be w.

Length of the rectangle = 2w + 5

Area of the rectangle given = 42 m²

Area of the rectangle = length × width

length × width = 42

(2w + 5) × w = 42

`2w^2+5w=42`

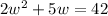
Subtract 42 from both sides, we get

`2w^2+5w-42=0`

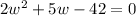
Using quadratic formula,

`$x=\frac{-b \pm \sqrt{b^(2)-4 a c}}{2 a}`

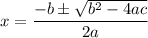
Here,
`a=2, b=5, c=-42`

`$w=\frac{-5 \pm \sqrt{5^(2)-4 \cdot 2(-42)}}{2 \cdot 2}`

`$w=(-5 \pm √(25+336))/(4)`

`$w=(-5 \pm √(361))/(4)`

`$w=(-5 \pm19)/(4)`

`$w=(-5+19)/(4), w=(-5-19)/(4)`

`$w=(14)/(4), w=(-24)/(4)`

`$w=(7)/(2), w=-6`

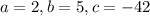
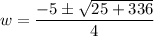
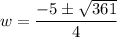
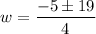
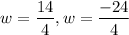
Dimension cannot be in negative, so neglect w = –6.

Width of the rectangle =
`(7)/(2)` m

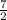`$L=2((7)/(2) )+5=12 \ m`

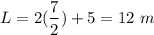
Hence length = 12 m and width =
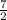`(7)/(2)` m.