Question

Please answer quickly I am running out of time

Answer 1

The value of
`g(-4)=(-4)/(3), \ g(-2)=3 \ \text{and} \ g(2)=(8)/(3)` .

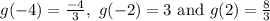Solution:

Given function:

`g(x)=\left\{\begin{array}{ll}-(1)/(3) x^(2)+4 & \text { if } x \\eq-2 \\3 & \text { if } x=-2\end{array}\right.`

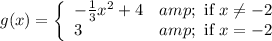
Substitute x = –4 in g(x), we get

`$g(-4) =- (1)/(3)(-4)^2+4`

`$=- (16)/(3)+4`

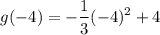
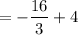
To make the denominator same, multiply and divide the 2nd term by 3.

`$=- (16)/(3)+(12)/(3)`

`$g(-4)=- (4)/(3)`

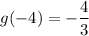
It is given that, if x = –2, then g(x) = 3

Therefore g(–2) = 3

Substitute x = 2 in g(x), we get

`$g(2) =- (1)/(3)(2)^2+4`

`$=- (4)/(3)+4`

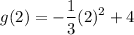
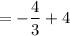
To make the denominator same, multiply and divide the 2nd term by 3.

`$=- (4)/(3)+(12)/(3)`

`$g(-2)= (8)/(3)`

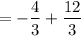
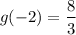
The value of
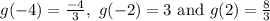`g(-4)=(-4)/(3), \ g(-2)=3 \ \text{and} \ g(2)=(8)/(3)` .