Question

Suppose 10000 people are given a medical test for a disease. About1% of all people have this condition. The test results have a 15% false positive rate and a 10% false negative rate. What percent of the people who tested positive actually have the disease?

Answer 1

The percent of the people who tested positive actually have the disease is 38.64%.

Explanation:

Denote the events as follows:

X = a person has the disease

P = the test result is positive

N = the test result is negative

Given:

`P(X)=0.01\\P(P|X^(c))=0.15\\P(N|X)=0.10`

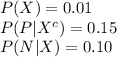
Compute the value of P (P|X) as follows:

`P(P|X)=1-P(P|X^(c))=1-0.15=0.85`

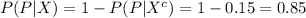
Compute the probability of a positive test result as follows:

`P(P)=P(P|X)P(X)+P(P|X^(c))P(X^(c))\\=(0.85*0.10)+(0.15*0.90)\\=0.22`

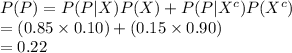
Compute the probability of a person having the disease given that he/she was tested positive as follows:

`P(X|P)=(P(P|X)P(X))/(P(P))=(0.85*0.10)/(0.22) =0.3864`

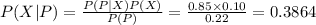
The percentage of people having the disease given that he/she was tested positive is, 0.3864 × 100 = 38.64%.